Bases Numéricas - Gustavo Guanabara

Estou começando este curso no dia 17 de Setembro de 2025

Comecei o curso e já terminei hoje mesmo! E tirei 100% na prova de primeira!

1ª Vídeo

Notação Posicional

17 de Setembro de 2025

Nesta aula inicial, o professor explica o conceito de notação posicional, mostrando como cada dígito de um número representa um valor diferente dependendo da sua posição. No sistema decimal (base 10), por exemplo, cada casa representa uma potência de 10 (unidades, dezenas, centenas, etc.). Exemplos como os números 2.004 e 123 ajudam a entender como funciona essa representação.

Em seguida, Guanabara faz a introdução ao sistema binário (base 2), usado pelos computadores, explicando que nele só existem dois dígitos: 0 e 1, representando os estados de ligado e desligado. A aula ensina como fazer a contagem correta em binário, mostrando que, assim como no decimal, é preciso esgotar todas as combinações antes de adicionar mais uma casa (por exemplo, de 1 para 10 no binário).

Outro ponto importante da aula é a conversão de números binários para decimais. O professor mostra o passo a passo para transformar um número como 1-0-1-1 em 11 na base decimal, usando o mesmo princípio da notação posicional: multiplicar cada dígito pela potência da base (2) e somar os resultados.

Essa base teórica é essencial para entender como funcionam as redes e o hardware.

2º Vídeo

Números Binários

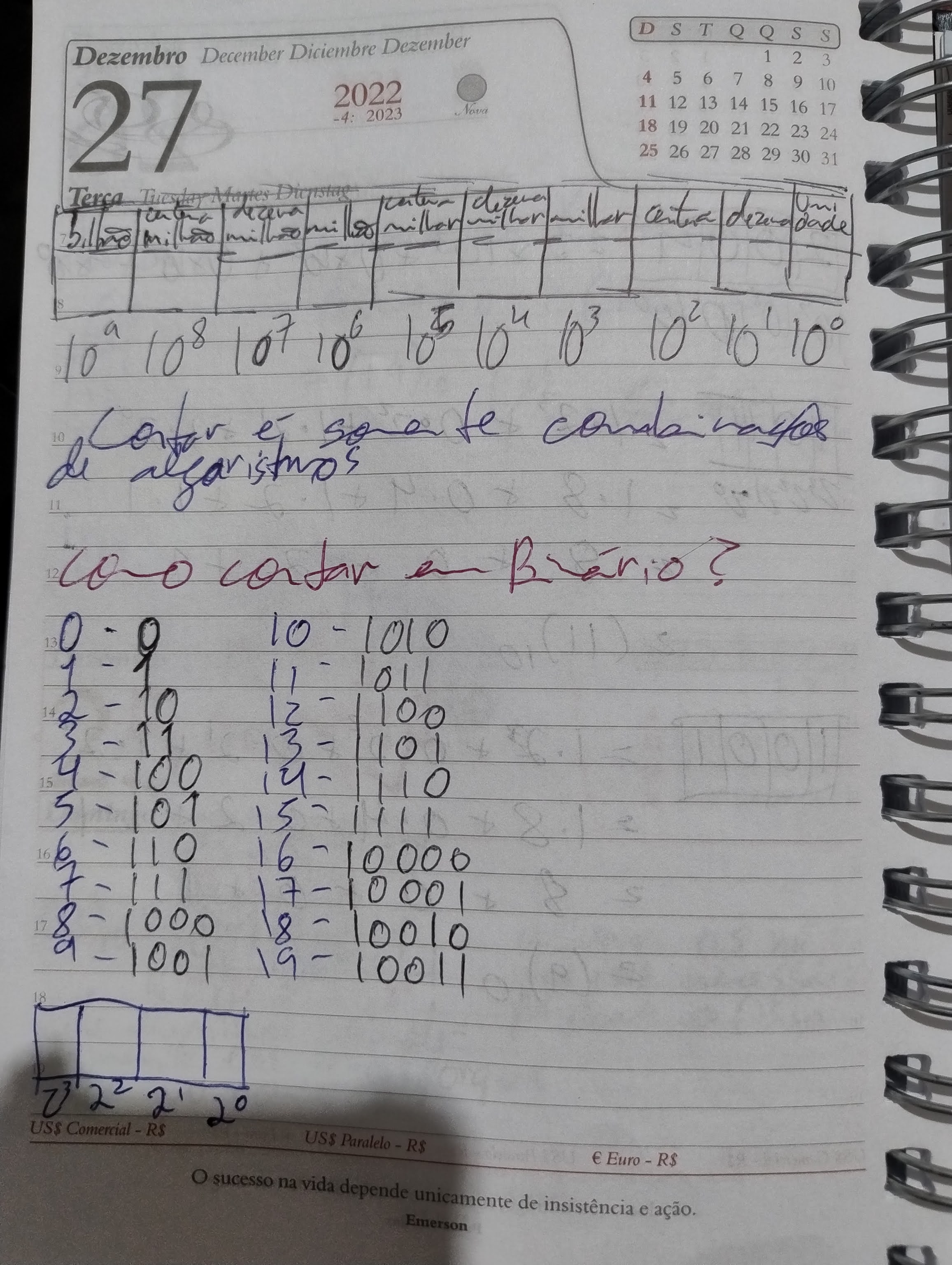
Nesta aula o professor Guanabara aprofunda um dos conceitos mais fundamentais da computação: a conversão entre os sistemas numéricos binário e decimal. Com uma abordagem didática e prática, ele retoma os principais pontos vistos anteriormente, explicando a diferença entre os sistemas de numeração: o decimal (base 10), usado pelos seres humanos, e o binário (base 2), essencial para os computadores, que funcionam por meio de sinais elétricos representando os estados ligado (1) e desligado (0).

O foco da aula está na conversão de binário para decimal, utilizando dois exemplos práticos: os números 1101 e 10011. O professor explica o método tradicional de conversão, baseado na multiplicação de cada dígito pelas suas respectivas potências de 2, e apresenta um macete visual, que facilita o processo ao somar apenas os valores das casas onde aparecem os dígitos 1.

Na sequência, Guanabara ensina como fazer a conversão de decimal para binário, utilizando também duas técnicas: a clássica divisão sucessiva por 2, com anotação dos restos e leitura invertida, e a técnica da seleção de potências de 2, onde o aluno identifica quais potências, somadas, resultam no número desejado, preenchendo uma tabela simples com 1s e 0s.

Durante a aula, o professor demonstra a aplicação das duas técnicas com os números 13 e 40, reforçando o aprendizado com a validação dos resultados por meio da conversão inversa. A aula termina com um convite à prática: os alunos são incentivados a testar os métodos com outros números e a realizar os exercícios disponíveis na plataforma.

Além de preparar os alunos para o próximo conteúdo — sistemas octal e hexadecimal —, a aula reforça a importância de entender o sistema binário para quem pretende trabalhar nas áreas de hardware, redes ou administração de sistemas, onde o conhecimento sobre endereçamento IP e representação binária é essencial.

Nessa aula vamos aprender a fazer uma conversão binário – decimal e decimal – binário usando dicas para acelerar o processo de conversão.

3º Vídeo

Números Octais e Hexadecimais

Nesta aula da série Hardware e Redes do Curso em Vídeo, o professor Guanabara apresenta dois novos sistemas numéricos muito utilizados na área de Tecnologia da Informação: o sistema octal (base 8) e o sistema hexadecimal (base 16). Ele começa relembrando o conteúdo das aulas anteriores sobre conversão de bases e reforça a importância de acompanhar o curso na sequência correta para não se perder nas explicações.

Guanabara destaca que o sistema octal utiliza os dígitos de 0 a 7, enquanto o sistema hexadecimal vai de 0 a 9, seguido pelas letras A a F, que representam os valores numéricos de 10 a 15. O professor chama a atenção para a importância de entender que essas letras têm valor numérico quando usadas no contexto hexadecimal, o que é fundamental para diversas aplicações em redes, hardware e programação.

Na sequência, ele revisa o conceito de notação posicional, explicando como calcular o valor decimal de um número representado em qualquer base, por meio da multiplicação de cada dígito pelas potências da base correspondente. Exemplos práticos ajudam a fixar o conteúdo: o número 371 (octal) é convertido para decimal, assim como o 1FA (hexadecimal).

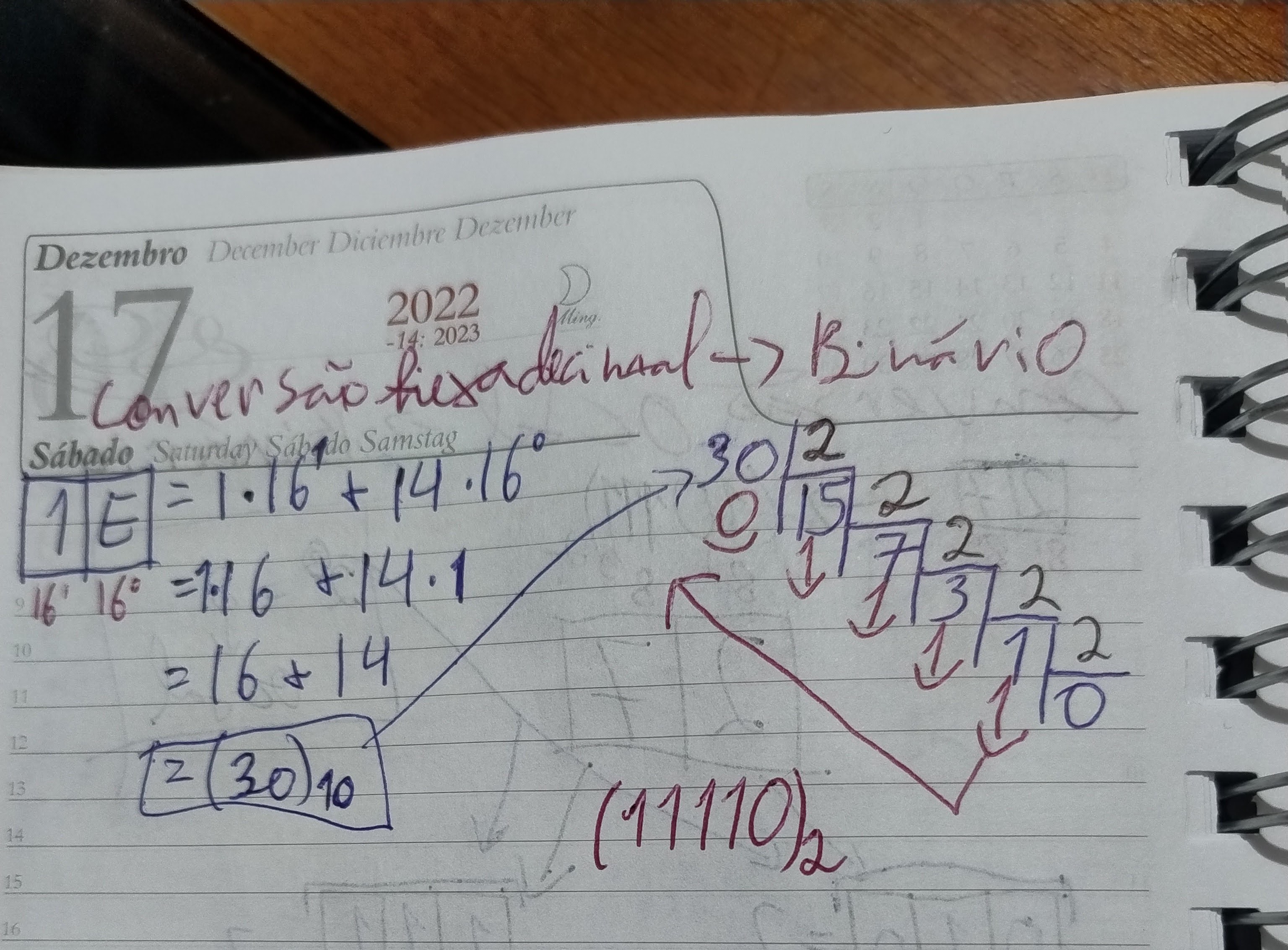
Além disso, a aula aborda o processo inverso: como converter de decimal para octal e de decimal para hexadecimal, usando o método das divisões sucessivas pela base, com anotação dos restos e leitura em ordem inversa. Para finalizar, Guanabara mostra como fazer a conversão de hexadecimal para binário, explicando que é necessário passar primeiro pelo decimal para depois chegar ao resultado em binário. O exemplo usado é o número 1E, que representa o decimal 30, que por sua vez vira o binário 11110.

O professor encerra a aula com um incentivo aos alunos: ele destaca que a prática constante é a melhor forma de fixar esse tipo de conteúdo.

4º Vídeo

Relações entre Sistemas de Numeração

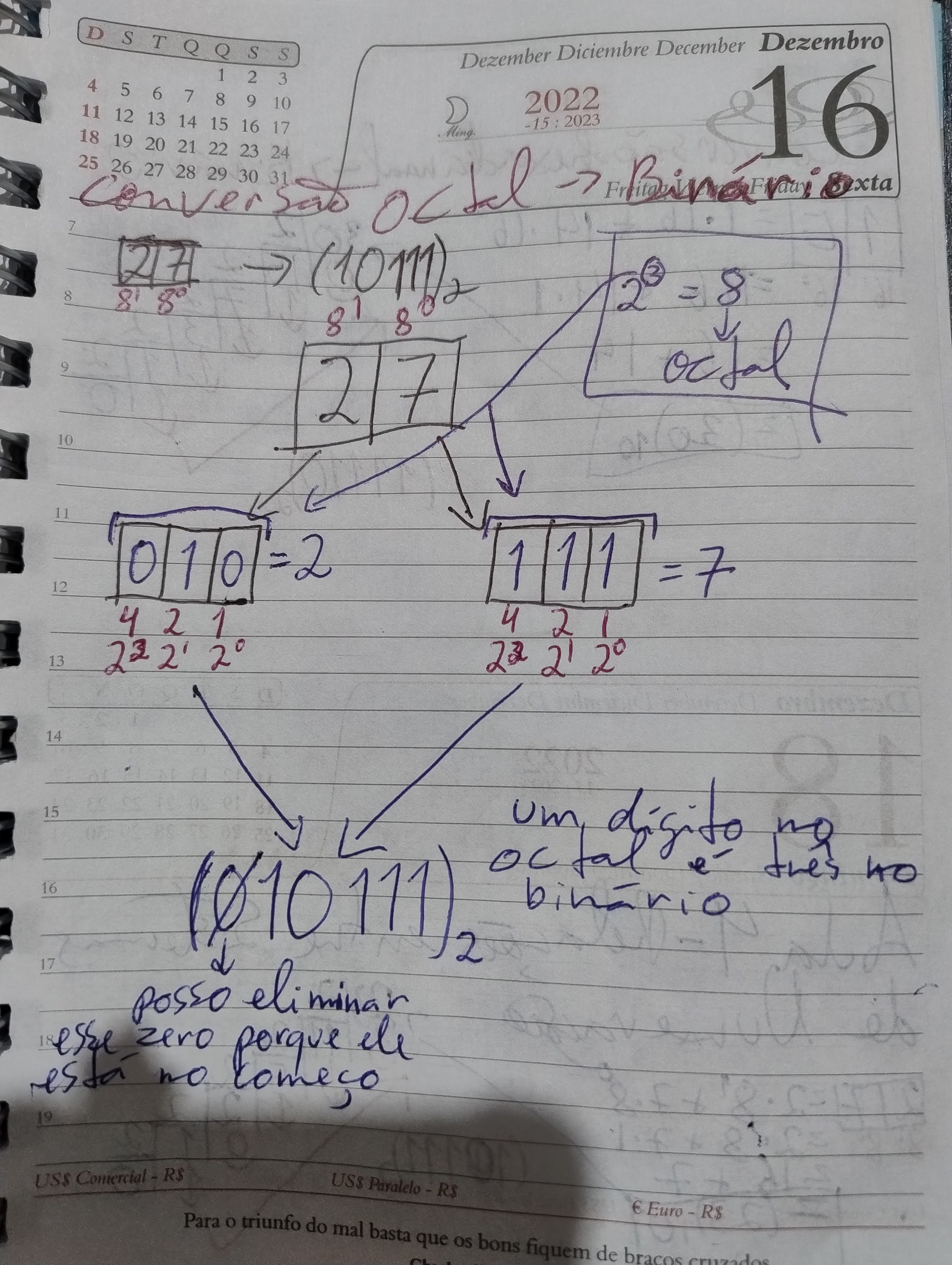
Nesta aula o professor Guanabara ensina técnicas rápidas e diretas para converter números entre as bases binária, octal e hexadecimal, sem a necessidade de passar pela base decimal. A proposta é facilitar a vida de quem trabalha ou estuda redes, hardware e programação, áreas onde a manipulação dessas bases é constante.

O professor começa revisando o método tradicional de conversão, que envolve passar primeiro para o decimal antes de chegar à base desejada. Como exemplo, ele converte o número 27 (octal) para binário utilizando essa abordagem. Em seguida, apresenta os macetes para conversão direta entre as chamadas “bases irmãs” (binário, octal e hexadecimal).

Para converter de binário para octal, a dica é dividir o número binário em grupos de três bits, da direita para a esquerda, completando com zeros à esquerda se necessário. Cada grupo é então convertido no dígito octal correspondente. No caso da conversão para hexadecimal, o processo é semelhante, mas feito com grupos de quatro bits, já que a base 16 é uma potência de 2⁴.

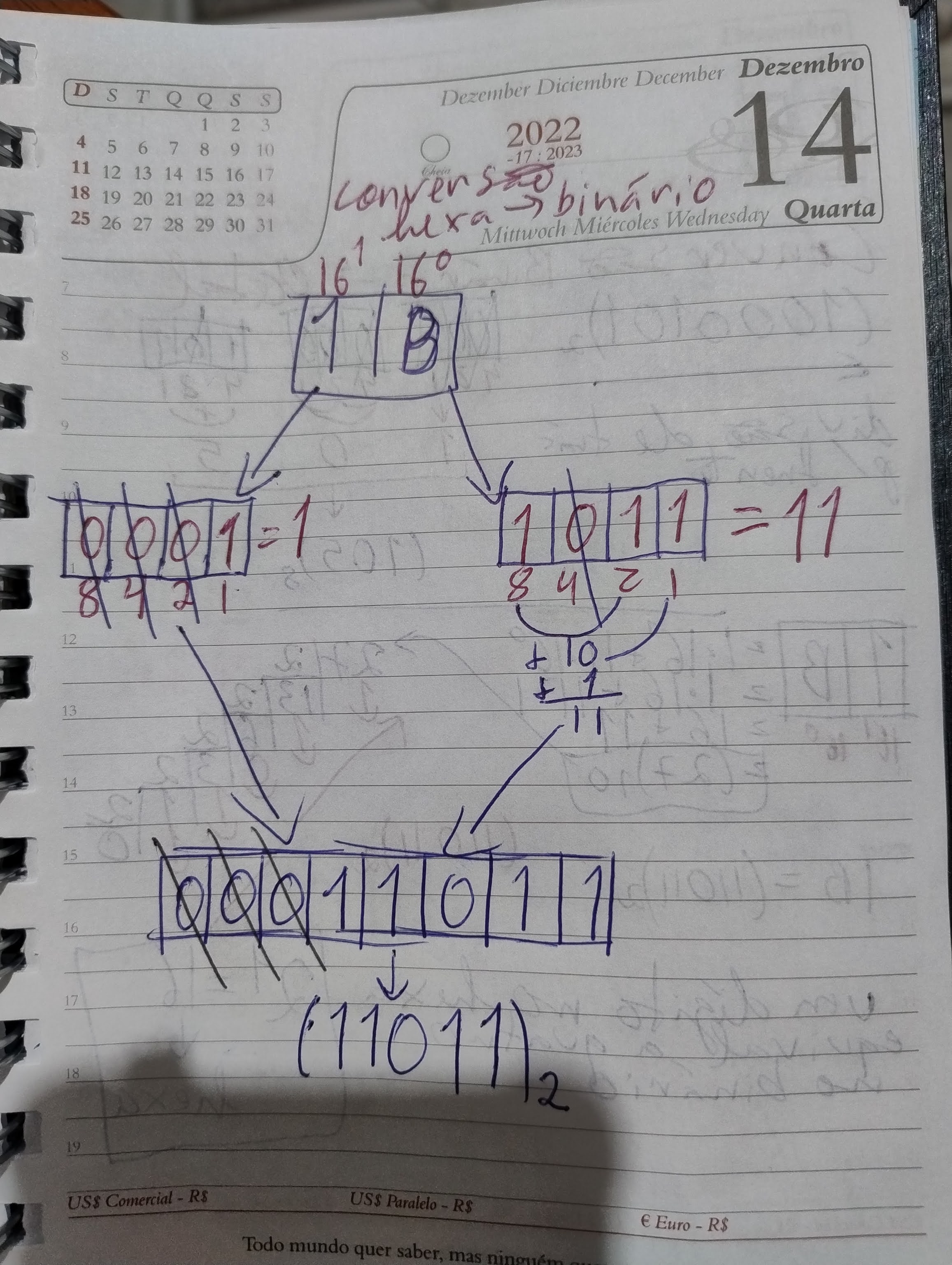
O professor também mostra o caminho inverso: de hexadecimal para binário, cada dígito hexadecimal se transforma em quatro bits binários, de forma direta e simples. Um exemplo prático apresentado foi a conversão do número “1B” (hexadecimal), que passa por decimal e depois para binário, além de mostrar como fazer a conversão direta apenas usando o agrupamento de bits.

Ao longo da aula, Guanabara reforça a importância de assistir às aulas na ordem certa, praticar bastante os exercícios e acessarem os materiais extras disponíveis no site.